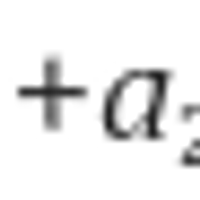비제차 선형 ODE : 매개변수 변화법, Variation of Parameters

 지금까지는 제차 선형 미분방정식의 일반해만 구했었다. 이번 글에서는 2계 비제차 선형 미분방정식을 푸는 방법 중 하나인 매개변수 변화법Variation of Parameters을 사용해 특수해를 구하고자 한다.

y₁과 y₂는 위의 식의 기저이다. 그러면 이번의 특수해는 기저에 상수가 아닌 u,v를 곱한 형태의 해를 생각하자.

이를 위 식에 대입하기 위해서 미분을 하자.

이 때, 이라고 가정하면 다음과 같이 식이 간단해진다.

한 번 더 미분하면,

이를 비제차 미분방정식에 대입하면,

초록색과 파란색의 문자는 제차의 해를 대입한 것이므로 0이 되기 때문에 없어진다.

그러면 아까 조건으로 삼았던  이것과 지금 나온 두 식을 연립하면 u'과 v'을 구할 수 있다. 즉,

이 연립 방정식의 해를 구하면 된다. 연립방정식은 아래와 같이 행렬로 쓸 수 있다.

---

연립방정식을 행렬로 풀기

왼쪽과 같은 연립방정식이 있다면 오른쪽과 같이 행렬로 쓸 수 있다. 앞의 2×2 행렬을 A라고 한다면, det A가 0이 아닐 때 아래의 A의 역행렬이 존재한다.

이 역행렬을 양변에 곱하면 x,y에 관한 식을 바로 얻을 수 있다. 

그런데 행렬 안에 있는 df-bg와 ag-fc는 아래와 같이 다시 쓸 수 있다.

따라서, x와 y는 아래처럼 구할 수 있다.

---

이제 우리가 구하고자 했던 연립방정식을 위와 같이 행렬로 다시 썼다. 이제 구하고자하는 u'과 v'는 아래와 같다.

이제 이 둘을 아래와 같이 간략히 쓰겠다.

그러면, u와 v는 이 둘을 적분하면 구할 수 있다.

따라서 맨 처음 구하고자 했던 형태의 특수해는 아래와 같다.

---

예) 의 일반해를 구하라.

먼저 제차의 해는 다음과 같다.

비제차의 특수해를 구하자. 먼저 W(y1,y2)의 값을 구하면,

그리고 W1과 W2의 값을 구하자.

이어서 u와 v를 구하자.

따라서 특수해는 다음과 같다.