여러가지 2계 선형 제차 미분방정식이 있지만, 그 중에서도 간단한 형태인 상수 계수를 갖는 것을 살펴보자.
위 식에서 a, b, c는 모두 상수이다. 그러면 위 식의 일반해를 구하는데,
정리를 하면 다음과 같이 된다.
위 식에서 지수 항이 0이 될 수 없으므로, aλ2 + bλ + c가 0이 되어야한다. 즉, 다음 식을 특성 방정식characteristic equation(또는 auxiliary equation)이라고 한다.
이제 근의 공식을 사용하여 λ를 구하면 된다. 그러면 경우의 수가 세가지가 있는데, 서로 다른 두 실근, 중근 그리고 서로 다른 허근이 나올 때 이다. 각각이 경우를 살펴보자.
서로 다른 두 실근, Two real roots (λ1≠λ2)
서로 다른 두 실근일 때는 해가 매우 간단하다.
y''-2y'-24y=0 의 일반해를 구하자.
위 미분방정식의 특성방정식은 다음과 같다.
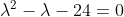
특성방정식의 해는 λ= 6, -4이다. 위 식의 일반해는, 다음과 같다.
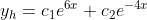
위 미분방정식의 특성방정식은 다음과 같다.
특성방정식의 해는 λ= 6, -4이다. 위 식의 일반해는, 다음과 같다.
특성 방정식이 중근으로 얻어졌을 때, 즉 λ=-b/2a 일 때는 한 해가 이미 정해졌다. 이때는 계수축소법,Reduction of order를 사용해서 다른 한 해를 구한다.
먼저 중근으로 얻어진 해는 다음과 같다.
계수축소법으로 다른 해를 구해보자.
따라서 일반해는 다음과 같다.
y''-2y'+y=0 의 일반해를 구하자.
위 미분방정식의 특성방정식은 다음과 같다.

특성방정식의 해는 λ= 1이다. 위 식의 일반해는, 다음과 같다.
 e^{x})
위 미분방정식의 특성방정식은 다음과 같다.
특성방정식의 해는 λ= 1이다. 위 식의 일반해는, 다음과 같다.
서로 다른 두 허근이 특성방정식의 해로 얻어졌다. 지수 부분에 허수가 들어가게 되는데, 우리는 복소수 함수를 원하지 않는다. 그래서 허수부를 없애기 위해서 Euler 공식, Euler's formular을 사용한다. Euler 공식, Euler's formular은 다음과 같다. 아래의 오일러 공식을 유도하는 방법은 많지만 이곳에서 다루진 않겠다.
서로 다른 두 허근은 λ1=α + βi, λ2=α - βi 이다. 그러면 두 해는 다음과 같다.
중첩의 원리로 위의 두 해를 더하고 뺀 후 나누어서, 허수부가 없는 새로운 두 해를 만든다. 그리고 이 새로운 두 해를 기저basis로 삼아 일반해를 만든다. 먼저 새로운 두 해는 다음과 같다.
따라서 일반해는 다음과 같이 얻어진다.
y''+2y'+3y=0 의 일반해를 구하자.
위 미분방정식의 특성방정식은 다음과 같다.

특성방정식의 해는 아래처럼 얻어진다.
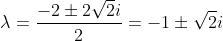
따라서, 위 미분방정식의 해는,
)
위 미분방정식의 특성방정식은 다음과 같다.
특성방정식의 해는 아래처럼 얻어진다.
따라서, 위 미분방정식의 해는,
'Mathematics > Ordinary Differential Equation' 카테고리의 다른 글
| Euler-Cauchy Equations (0) | 2014.07.27 |
|---|---|
| 질량과 용수철-자유진동 (1) | 2014.07.22 |
| 계수 축소법 Reduction of order (2) | 2012.01.17 |
| 2계 선형 미분방정식, Second-Order Linear ODE (0) | 2012.01.13 |
| Bernoulli differential equation 베르누이 미분 방정식 (1) | 2012.01.07 |

