One dimensional free particle motion

1차원 자유 입자(free particle)에 대해서 생각해보자. 자유 입자란 입자의 운동을 방해하거나 도와주는 힘인 퍼텐셜 에너지가 없다는 것이다. 퍼텐셜 에너지가 없다는 것은 V(x)=0 이란 뜻이다. 이에 따라 Schrodinger 방정식을 세우면,

이를 정리하여 표준형으로 만들면,

 

각 함수 앞의 계수가 상수이므로, 해를 로 가정하고 대입하여 풀자.

따라서,
 이고,  가 된다. 만약 여기서,  이라면, 파동함수가 0이라는 뜻이 되고, 이는 입자가 없다는 뜻이 되므로 가 되어야 한다.

그래서 파동함수의 해는

가 되며, 중첩의 원리에 의해

 

가 되는데 이것이 해가 된다.

이를 간략히 쓰기 위해서,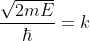 로 치환하면,

가 된다.

그리고 이때의 에너지, E는 다음과 같다.

 

---

The probability density

 - 만약 B=0 이라면, 가 된다.
그리고 확률 밀도 함수는

이 되며,
상수만 남게 된다.

즉, 이에 대해 그래프를 그려보면

위의 그래프처럼 되는데,
이는 위치 x에 상관없이 어느 곳에서나 자유입자를 발견할 확률이 동일하다는 뜻이 된다.

- 만약 A=0 이여도 결론은 B=0일때와 같아질 것이다.


- A=B 이라면 파동함수는  이 되고,
Euler식에 의해 파동함수는 다음과같이 바뀌게 된다.

확률 밀도 함수는 파동함수를 제곱한 것이므로 다음과 같다.

이를 그래프로 그려보면,

이는, 위치 x에 따라 발견할 확률이 달라지며 발견할 확률이 없는 곳(ψ² = 0)도 있다.