계의 상태의 미소 변화와 내부 에너지의 미소변화 dU를 살펴보자. 만약 계에 행해진 일이 dw이고 열로서 공급된 에너지가 dq라고 하자. 그러면  을 다음과 같이 바꿔쓸 수 있다.
을 다음과 같이 바꿔쓸 수 있다.
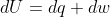
이 식을 사용하려면 dq와 dw를 구할 수 있어야 한다. 우선 부피 변화에 기인하는 일인 팽창 일(Expansion work)부터 생각하자.
일, Work
팽창 일은 물리학의 정의에 따라 계산 해야한다. 어떤 물체를 힘 F인 대립하는 힘에 맞서서 dz 만큼의 거리를 이동시키는데 필요한 일은 다음과 같이 정의된다.
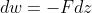
음의 부호가 붙게 되는 이유는 계가 힘에 맞서서 물체를 이동시키면 계의 내부 에너지가 감소된다는 사실을 표현하기 위한 것이다.
면적이 A인 피스톤에서 외부압력이 Pex인 상태에서 피스톤이 dz의 거리만큼 움직인 과정에 대한 팽창일은 다음과 같다.

압력과 면적을 곱하면 힘이 된다. 즉 압력 P의 단위는 N/m²이고 면적은 m²이므로 P*A는 N이 되어 힘이된다. 그리고, P*V는 Nm가 되어 J 즉, 에너지의 단위가 된다. 부피가 Vi에서 Vf로 변할 때 전체 팽창일은 다음 식처럼 적분해서 구한다.

자유 팽창, Free expansion
Pex=0 인 팽창을 자유 팽창이라고 말한다. 진공 속으로 팽창될 때 자유 팽창에서 계에 행해지는 일 w = 0 이다. 그 이유는 바로 위의 식에 Pex=0를 넣고 적분하면 자명해진다.

일정 외부 압력하에서의 팽창, Expansion against constant pressure
Pex= 일정인 상태에서의 팽창을 비가역 팽창이라고 한다. 또는 일정한 외부 압력하에서의 팽창, 기체가 한 단계로 팽창했다고도 표현한다. 일정한 대기압에 대해서 팽창하는 것이 비가역 팽창의 예이다. 비가역 팽창은 V에 대해 Pex가 일정하므로 적분의 바깥으로 튀어져나오며 적분은 V의 변화량이 된다. 따라서, 이때의 일은 다음과 같다.

가역 팽창, Reversible expansion
가역 변화(Reversible change)란 임의의 물리적 상태에 있는 계에 특정 변수를 미소하게 변화시켜서 그 변화를 역방향으로 일어나게 할 수 있는 변화를 뜻한다. 이때 반대 방향으로 특정 변수를 미소하게 변화시켰을 때, 계의 상태가 반대 방향으로 변화하면 그 계는 주위와 평형(equilibrium)상태에 있다고 말한다.
가역적 팽창이 일어나게 하려면 각 팽창 단계마다 외부 압력 Pex가 계의 내부 압력 P와 같게 해주어야 한다. 이러한 가역 과정을 준평형과정(quasi-equilibrium process) 또는 준정지과정 (quasi-static process)이라 부른다.

위의 적분식을 구하려면 계의 내부 기체의 압력이 부피 변화에 대해 어떻게 의존하는지 알아야한다. 만약 기체가 이상기체 상태식을 따른다면 가역 팽창에서의 일은,

등온 가역 팽창, Isothermal reversible expansion
계의 온도를 주위의 온도와 열적 평형인 상태를 유지하면서 일어나는 팽창을 말한다. 그러면 온도는 부피V에 의존하지 않고 상수가 되어 바로 위식에서는 적분의 바깥으로 나갈 수 있다.

이 식을 사용하려면 dq와 dw를 구할 수 있어야 한다. 우선 부피 변화에 기인하는 일인 팽창 일(Expansion work)부터 생각하자.
팽창 일은 물리학의 정의에 따라 계산 해야한다. 어떤 물체를 힘 F인 대립하는 힘에 맞서서 dz 만큼의 거리를 이동시키는데 필요한 일은 다음과 같이 정의된다.
음의 부호가 붙게 되는 이유는 계가 힘에 맞서서 물체를 이동시키면 계의 내부 에너지가 감소된다는 사실을 표현하기 위한 것이다.
면적이 A인 피스톤에서 외부압력이 Pex인 상태에서 피스톤이 dz의 거리만큼 움직인 과정에 대한 팽창일은 다음과 같다.
압력과 면적을 곱하면 힘이 된다. 즉 압력 P의 단위는 N/m²이고 면적은 m²이므로 P*A는 N이 되어 힘이된다. 그리고, P*V는 Nm가 되어 J 즉, 에너지의 단위가 된다. 부피가 Vi에서 Vf로 변할 때 전체 팽창일은 다음 식처럼 적분해서 구한다.
Pex=0 인 팽창을 자유 팽창이라고 말한다. 진공 속으로 팽창될 때 자유 팽창에서 계에 행해지는 일 w = 0 이다. 그 이유는 바로 위의 식에 Pex=0를 넣고 적분하면 자명해진다.
Pex= 일정인 상태에서의 팽창을 비가역 팽창이라고 한다. 또는 일정한 외부 압력하에서의 팽창, 기체가 한 단계로 팽창했다고도 표현한다. 일정한 대기압에 대해서 팽창하는 것이 비가역 팽창의 예이다. 비가역 팽창은 V에 대해 Pex가 일정하므로 적분의 바깥으로 튀어져나오며 적분은 V의 변화량이 된다. 따라서, 이때의 일은 다음과 같다.
가역 변화(Reversible change)란 임의의 물리적 상태에 있는 계에 특정 변수를 미소하게 변화시켜서 그 변화를 역방향으로 일어나게 할 수 있는 변화를 뜻한다. 이때 반대 방향으로 특정 변수를 미소하게 변화시켰을 때, 계의 상태가 반대 방향으로 변화하면 그 계는 주위와 평형(equilibrium)상태에 있다고 말한다.
가역적 팽창이 일어나게 하려면 각 팽창 단계마다 외부 압력 Pex가 계의 내부 압력 P와 같게 해주어야 한다. 이러한 가역 과정을 준평형과정(quasi-equilibrium process) 또는 준정지과정 (quasi-static process)이라 부른다.
위의 적분식을 구하려면 계의 내부 기체의 압력이 부피 변화에 대해 어떻게 의존하는지 알아야한다. 만약 기체가 이상기체 상태식을 따른다면 가역 팽창에서의 일은,
계의 온도를 주위의 온도와 열적 평형인 상태를 유지하면서 일어나는 팽창을 말한다. 그러면 온도는 부피V에 의존하지 않고 상수가 되어 바로 위식에서는 적분의 바깥으로 나갈 수 있다.
'Physical Chemistry > Thermodynamics' 카테고리의 다른 글
| 엔탈피, Enthalpy (2) | 2011.02.02 |
|---|---|
| 열의 이전, Heat transactions (1) | 2011.01.01 |
| 열역학 제1법칙, First Law of thermodynamics (3) | 2010.12.24 |
| van der Waals 상태식 & 대응상태의 원리 (3) | 2010.12.24 |
| 분자 상호작용 (3) | 2010.11.12 |


