수소 원자에 대한 Schrodinger equation을 풀면 네 개의 양자수(n, l, ml, ms)를 얻는다. 이 네 개의 양자수에 의해서 각 전자의 에너지, 각운동량, 분포, 스핀 상태가 결정된다. 그리고 네 개의 양자수를 하나의 양자 상태로 보고, 각 양자 상태에 대한 기호도 1s, 2s, 2p, 3s, 3p, 3d 식으로 결정이 되었었다. Bohr model에서는 각 전자가 정해진 궤도orbit을 돌고, 다른 궤도와의 에너지에 해당하는 빛을 흡수하거나 방출 했을 때만 전자가 다른 궤도로 돈다고 했었다. 하지만, Schrodinger equation에 따르면 전자는 확실하게 정해진 궤도orbit가 아닌 마치 구름과 같이 어느정도 흩어져있는 분포를 보인다. 그래서 우리는 이것이 궤도와는 다르기에 궤도함수Orbital라고 이름 붙인다.
s 오비탈 s orbital
수소 원자에 대한 Schrodinger equation을 풀면 s 오비탈에 대한 파동함수를 구할 수 있다. s 오비탈은 모든 주양자수 n에 대해서 있으며, 그중에서도 부양자수 l의 값이 0인 것이다. 파동함수에서 Zr/a0를 σ라고 정의하겠다. 여기서 Z는 수소꼴 원자의 양성자 갯수, r은 핵-전자간 거리(변수), a0는 52.9pm에 해당하는 상수로 Bohr 반지름Bohr radius 이다.
^{\frac{1}{2}}} e^{-\sigma } "\psi _{1s} = \frac{Z^{3/2}}{(\pi a_0^3)^{\frac{1}{2}}} e^{-\sigma }")
 e^{-\sigma /2} "\psi _{2s} = \frac{1}{4\sqrt{2\pi}}\left [\frac{Z}{a_0} \right ]^{3/2}(2-\sigma ) e^{-\sigma /2}")
 e^{-\sigma /3} "\psi _{3s} = \frac{1}{81\sqrt{3\pi}}\left [\frac{Z}{a_0} \right ]^{3/2}(27-18\sigma + 2\sigma ^2 ) e^{-\sigma /3}")
위 식들은 r에 대한 함수일 뿐, θ나 φ의 함수는 아니다. 즉, 핵-전자간 거리의 함수이며 각도 의존성은 없다. 즉 구형대칭이다. 이를 그래프로 그리면 다음과 같이 된다.
● Radial distribution function
전자가 r에서 r+dr 사이의 작은 부피 내에서 발견될 확률을 구해보자.
r에서부터 r+dr 사이의 부피는 다음과 같다.
^3-\frac{4}{3}\pi r^3 = 4\pi r^2dr + 4\pi r(dr)^2 + \frac{4}{3}\pi (dr)^3 \simeq 4\pi r^2 dr "\frac{4}{3}\pi (r+dr)^3-\frac{4}{3}\pi r^3 = 4\pi r^2dr + 4\pi r(dr)^2 + \frac{4}{3}\pi (dr)^3 \simeq 4\pi r^2 dr")
dr은 굉장히 작은 구간이고 r에 비해 무시할 수 있을만큼 작기에 dr의 제곱과 세제곱항은 무시해도 괜찮다. s 오비탈에서는 부피와 그곳에서의 파동함수의 제곱의 곱이 바로 발견할 확률이 된다. 이를 Raidal distribution function P(r) 이라고 한다.
 = 4\pi r^2 \psi ^2 "P(r) = 4\pi r^2 \psi ^2")
이제 P(r)의 그래프를 그리면 다음과 같이 된다.
P2s(r)을 보면 0이 아닌 곳에서 발견할 확률이 0인 곳이 있다. 이렇게 발견할 확률이 0인 지점을 마디node라고 한다. 일반적으로 Rn,l(r) 함수의 node의 수는 n-l-1 로 주어진다.
그리고 P1s(r)에서 발견할 확률이 최대인 지점은 함수를 r에 대해서 미분하여 0이 되는r 값을 찾으면 되는데, r=a0로 주어진다.
p 오비탈 p orbital
p 오비탈은 n≥2 이상일 때의 l=1 인 경우이므로 L shell 부터 존재한다. p 오비탈부터는 전체 파동함수 중에서 Radial wave function을 뺀 구면 조화 함수Spherical harmonics Yl,ml(θ,φ)만으로 표시하겠다.
= (\frac{3}{4\pi})^{1/2}cos \theta "Y_{1,0}(\theta ,\phi )= (\frac{3}{4\pi})^{1/2}cos \theta")
= - (\frac{3}{8\pi})^{1/2}sin \theta e^{i\phi } "Y_{1,1}(\theta ,\phi )= - (\frac{3}{8\pi})^{1/2}sin \theta e^{i\phi }")
= (\frac{3}{8\pi})^{1/2}sin \theta e^{-i\phi } "Y_{1,-1}(\theta ,\phi )= (\frac{3}{8\pi})^{1/2}sin \theta e^{-i\phi }")
위의 식은 2p 오비탈을 표현하는 구면 조화 함수이다.
Y1,1와 Y1,-1는 식에 허수 i를 포함하고 있다. 허수 i를 없애기 위해서 Euler's Fomula, Euler 관계식을 사용하자.
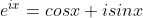
Euler 관계식
Euler 관계식을 사용하면, Y1,1와 Y1,-1는 다음과 같이 된다.
^{1/2}sin\theta (cos\phi + i sin\phi) "Y_{1,1}= -(\frac{3}{8\pi})^{1/2}sin\theta (cos\phi + i sin\phi)")
^{1/2}sin\theta (cos\phi - i sin\phi) "Y_{1,-1}= (\frac{3}{8\pi})^{1/2}sin\theta (cos\phi - i sin\phi)")
이제 두 식을 더하거나 빼는 중첩Superposition하여 새로운 파동함수 두개를 만들자.
=(\frac{3}{8\pi})^{1/2}sin\theta sin\phi "-\frac{1}{2i}(Y_{1,1}+Y_{1,-1})=(\frac{3}{8\pi})^{1/2}sin\theta sin\phi")
=(\frac{3}{8\pi})^{1/2}sin\theta cos\phi "-\frac{1}{2}(Y_{1,1}-Y_{1,-1})=(\frac{3}{8\pi})^{1/2}sin\theta cos\phi")
그러면 이제 허수부가 없는 파동함수 세 개가 얻어졌다. 이제 각 파동함수에 일정한 기호를 붙이는데, 규칙은 다음과 같다. x=rsinθcosφ , y=rsinθcosθ, z=rcosθ 이다. Y1,0은 cosθ 만 있으므로 pz 가 된다. 이런식으로 이름을 붙이면 px 와 py 도 만들 수 있다.
=(\frac{3}{8\pi})^{1/2}sin\theta cos\phi \Rightarrow p_x "-\frac{1}{2}(Y_{1,1}-Y_{1,-1})=(\frac{3}{8\pi})^{1/2}sin\theta cos\phi \Rightarrow p_x")
=(\frac{3}{8\pi})^{1/2}sin\theta sin\phi \Rightarrow p_y "\frac{1}{2i}(Y_{1,1}+Y_{1,-1})=(\frac{3}{8\pi})^{1/2}sin\theta sin\phi \Rightarrow p_y")
^{1/2}cos\theta \Rightarrow p_z "Y_{1,0}= (\frac{3}{4\pi})^{1/2}cos\theta \Rightarrow p_z")
d 오비탈 d orbital
d 오비탈들은 n≥3이상의 l=2인 것으로 M 껍질에서부터 나타난다.
^{1/2} (3cos^2\theta -1 ) \rightarrow d_{z^2} "Y_{2,0}= (\frac{5}{16\pi})^{1/2} (3cos^2\theta -1 ) \rightarrow d_{z^2}")
^{1/2}cos\theta sin\theta e^{i\phi} =-(\frac{5}{16\pi})^{1/2}cos\theta sin\theta (cos\phi + isin\phi) \\ \\ Y_{2,-1}= (\frac{5}{16\pi})^{1/2}cos\theta sin\theta e^{-i\phi} =(\frac{5}{16\pi})^{1/2}cos\theta sin\theta (cos\phi - isin\phi) \end{matrix}\right\} "\left.\begin{matrix} Y_{2,1}= -(\frac{5}{16\pi})^{1/2}cos\theta sin\theta e^{i\phi} =-(\frac{5}{16\pi})^{1/2}cos\theta sin\theta (cos\phi + isin\phi) \\ \\ Y_{2,-1}= (\frac{5}{16\pi})^{1/2}cos\theta sin\theta e^{-i\phi} =(\frac{5}{16\pi})^{1/2}cos\theta sin\theta (cos\phi - isin\phi) \end{matrix}\right\}")
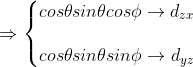
^{1/2} sin^2\theta e^{2i\phi} = (\frac{5}{16\pi})^{1/2} sin^2\theta (cos2\phi + isin2\phi) \\ \\ Y_{2,-2}= (\frac{5}{16\pi})^{1/2} sin^2\theta e^{-2i\phi} =(\frac{5}{16\pi})^{1/2} sin^2\theta (cos2\phi - isin2\phi) \end{matrix}\right\} "\left.\begin{matrix} Y_{2,2}= (\frac{5}{16\pi})^{1/2} sin^2\theta e^{2i\phi} = (\frac{5}{16\pi})^{1/2} sin^2\theta (cos2\phi + isin2\phi) \\ \\ Y_{2,-2}= (\frac{5}{16\pi})^{1/2} sin^2\theta e^{-2i\phi} =(\frac{5}{16\pi})^{1/2} sin^2\theta (cos2\phi - isin2\phi) \end{matrix}\right\}")
 \rightarrow d_{x^2-y^2} \\ \\ sin^2\theta sin2\phi \rightarrow 2sin^2 \theta sin\phi cos\phi \rightarrow d_{xy} \end{matrix}\right. "\Rightarrow \left\{\begin{matrix} sin^2\theta cos2\phi \rightarrow sin^2\theta (cos^2\phi - sin^2\phi ) \rightarrow d_{x^2-y^2} \\ \\ sin^2\theta sin2\phi \rightarrow 2sin^2 \theta sin\phi cos\phi \rightarrow d_{xy} \end{matrix}\right.")
수소 원자에 대한 Schrodinger equation을 풀면 s 오비탈에 대한 파동함수를 구할 수 있다. s 오비탈은 모든 주양자수 n에 대해서 있으며, 그중에서도 부양자수 l의 값이 0인 것이다. 파동함수에서 Zr/a0를 σ라고 정의하겠다. 여기서 Z는 수소꼴 원자의 양성자 갯수, r은 핵-전자간 거리(변수), a0는 52.9pm에 해당하는 상수로 Bohr 반지름Bohr radius 이다.
위 식들은 r에 대한 함수일 뿐, θ나 φ의 함수는 아니다. 즉, 핵-전자간 거리의 함수이며 각도 의존성은 없다. 즉 구형대칭이다. 이를 그래프로 그리면 다음과 같이 된다.
[왼쪽부터 1s, 2s, 3s에 해당하는 Radial wave function.]
● Radial distribution function
전자가 r에서 r+dr 사이의 작은 부피 내에서 발견될 확률을 구해보자.
r에서부터 r+dr 사이의 부피는 다음과 같다.
dr은 굉장히 작은 구간이고 r에 비해 무시할 수 있을만큼 작기에 dr의 제곱과 세제곱항은 무시해도 괜찮다. s 오비탈에서는 부피와 그곳에서의 파동함수의 제곱의 곱이 바로 발견할 확률이 된다. 이를 Raidal distribution function P(r) 이라고 한다.
이제 P(r)의 그래프를 그리면 다음과 같이 된다.
P2s(r)을 보면 0이 아닌 곳에서 발견할 확률이 0인 곳이 있다. 이렇게 발견할 확률이 0인 지점을 마디node라고 한다. 일반적으로 Rn,l(r) 함수의 node의 수는 n-l-1 로 주어진다.
그리고 P1s(r)에서 발견할 확률이 최대인 지점은 함수를 r에 대해서 미분하여 0이 되는r 값을 찾으면 되는데, r=a0로 주어진다.
p 오비탈은 n≥2 이상일 때의 l=1 인 경우이므로 L shell 부터 존재한다. p 오비탈부터는 전체 파동함수 중에서 Radial wave function을 뺀 구면 조화 함수Spherical harmonics Yl,ml(θ,φ)만으로 표시하겠다.
위의 식은 2p 오비탈을 표현하는 구면 조화 함수이다.
Y1,1와 Y1,-1는 식에 허수 i를 포함하고 있다. 허수 i를 없애기 위해서 Euler's Fomula, Euler 관계식을 사용하자.
Euler 관계식
Euler 관계식을 사용하면, Y1,1와 Y1,-1는 다음과 같이 된다.
이제 두 식을 더하거나 빼는 중첩Superposition하여 새로운 파동함수 두개를 만들자.
그러면 이제 허수부가 없는 파동함수 세 개가 얻어졌다. 이제 각 파동함수에 일정한 기호를 붙이는데, 규칙은 다음과 같다. x=rsinθcosφ , y=rsinθcosθ, z=rcosθ 이다. Y1,0은 cosθ 만 있으므로 pz 가 된다. 이런식으로 이름을 붙이면 px 와 py 도 만들 수 있다.
[2p, 3p 오비탈]
d 오비탈들은 n≥3이상의 l=2인 것으로 M 껍질에서부터 나타난다.
'Physical Chemistry > Quantum Chemistry' 카테고리의 다른 글
| 분자 구조-원자가 결합 이론, Molecular Structure-Valence bond theory (2) | 2012.03.10 |
|---|---|
| 다전자 원자의 구조, The Structures of many-electron atoms (2) | 2012.01.22 |
| 수소 원자의 구조 (1) | 2011.08.22 |
| Rotation in Three Dimensions, 3차원 회전 운동 (0) | 2011.08.16 |
| Rotation in Two Dimensions, 이차원 회전 운동 (0) | 2011.06.29 |
