함수의 극한

해당 글을 새로 다시 썼습니다.
아래를 클릭하면 새로운 글로 이동합니다.
http://joonyoungsun.tistory.com/entry/함수의-극한-Limit-of-a-Function

---

Def. 극한
극한, 즉
의 엄밀한 정의는
', 에 대하여 가 성립하는 이 존재한다.'

하지만 우선은 이 정의는 다루지 않고 극한의 의미를 직관적으로만 생각한다.

극한의 의미
 함수 에서 가 의 오른쪽에서(가 보다 큰 쪽에서) 에 가까워짐에 따라 가 에 가까워진다고 하자.
이를 기호로

로 나타내고, 이때 값 를 의 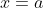에서의 우극한(right-hand limit)이라 한다.

반대로 가 의 왼쪽에서(가 보다 작은 쪽에서) 에 가까워짐에 따라 가 에 가까워진다고 하자.
이를 기호로

 

로 나타내고, 이때 값 를 의 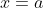에서의 좌극한(left-hand limit)이라 한다.

그리고 우극한과 좌극한이 같은 값 로 가까워지면

 

으로 나타내고, 을 의 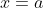에서의 극한(limit)이라고 한다.

Thm 1.3.1
함수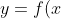 와 가 모두 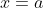에서 극한을 갖는다고 하고, 그 극한을 각각 , 라고 하자.
즉, 이라 하자.
이때 다음 식이 성립한다.

1.   (는 임의의 상수)
2.
3.
4.이라면,
5. 일 때,

합성함수 극한에 대하여 다음 성질이 성립한다.
6. 만약 이면,