평균 변화율
함수
즉,-a=h,\; \Delta y=f(a+h)-f(a)) 이다.
이다.
그리고

즉,

그리고 ) 의 기하학적 의미는 그림 2에서와 같이
의 기하학적 의미는 그림 2에서와 같이 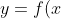) 의 그래프에서
의 그래프에서  에서의 접선(tangent line)의 기울기를 나타낸다.
에서의 접선(tangent line)의 기울기를 나타낸다. ) 가 존재하면
가 존재하면 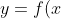) 는
는  에서 미분 가능(differentiable)하다고 하며,
에서 미분 가능(differentiable)하다고 하며, ) 를 다음과 같이 표현할 수 있다.
를 다음과 같이 표현할 수 있다.
Thm 2.1.1
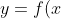) 가
가  에서 미분 가능하면,
에서 미분 가능하면,  에서 연속이다.
에서 연속이다.
※증명
![\100dpi \lim_{x\to a}f(x)=f(a)\rightarrow \lim_{x\to a}[f(x)-f(a)] = \lim_{x\to a}\frac{f(x)-f(a)}{x-a}(x-a)](http://latex.codecogs.com/gif.latex?\100dpi \lim_{x\to a}f(x)=f(a)\rightarrow \lim_{x\to a}[f(x)-f(a)] = \lim_{x\to a}\frac{f(x)-f(a)}{x-a}(x-a))
\times 0=0)
=f(a))
도함수
=\lim_{h\to o}\frac{f(x+h)-f(x)}{h}) 이렇게 얻어진 함수
이렇게 얻어진 함수 ) 를
를 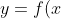) 의 도함수(derivative)라고 하며, 기호로
의 도함수(derivative)라고 하며, 기호로 ) ,
, 로 표시한다.
로 표시한다.
이런 도함수를 구하는 과정을 미분하다(differentiate)라고 한다.
※증명
이런 도함수를 구하는 과정을 미분하다(differentiate)라고 한다.
'Mathematics > General Mathematics' 카테고리의 다른 글
| 수열, Sequence (0) | 2012.04.30 |
|---|---|
| 여러가지 미분법 (1) | 2009.11.05 |
| 함수의 연속 (1) | 2009.11.04 |
| 함수의 극한 (0) | 2009.11.04 |
| 함수 (0) | 2009.11.04 |