미분적분학에서 미분은 함수가 얼만큼 변화하는지 측정하는 방법이다. 넓게 표현하면, 미분은 어떤 양이 변화할 때 그에 대응해서 다른 양이 얼만큼 변화하는지 생각하는 것이다. 그 예로 시간이 지남에 따라 물체의 위치에 대해 미분을 하면 물체의 순간 속도가 된다.
도함수를 찾는 과정을 미분differentiation이라고 한다. 이의 역과정을 역도함수antidifferentiation, 부정적분indefinite integral이라고 한다. 미적분학의 기본 정리는 역도함수가 적분과 같다고 말한다. 미분과 적분은 단일 변수 미적분학의 두개의 기본 연산이다.
여러 함수들의 미분을 다루는데 있어 가장 기본이 되는 다항식의 미분을 생각해보자.
n∈N 일 때, 함수 f(x)=xn 이라고 하자. 그러면 f'(x)는 정의에 따라,
=Dx^{n}=\lim_{h\to%200}\frac{f(x+h)-f(x)}{h}=\lim_{h\to%200}\frac{(x+h)^{n}-x^{n}}{h})
가 된다.
다항함수를 전개하면,
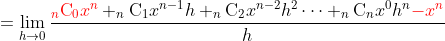
빨갛게 표시한 항은 같으므로 0이 되고 h 항을 중심으로 정리하면,
![{\color{red} }=\lim_{h\to 0}\frac{{\color{red} h}}{{\color{red} h}}\, [nx^{n-1}+\frac{n(n+1)}{2}x^{n-2}{\color{red} h}+\frac{n(n+1)(n+2)}{6!}x^{n-3}{\color{red} h^{2}}\cdots +{\color{red} h^{n-1}}]](http://latex.codecogs.com/gif.latex?{\color{red}%20}=\lim_{h\to%200}\frac{{\color{red}%20h}}{{\color{red}%20h}}\,%20[nx^{n-1}+\frac{n(n+1)}{2}x^{n-2}{\color{red}%20h}+\frac{n(n+1)(n+2)}{6!}x^{n-3}{\color{red}%20h^{2}}\cdots%20+{\color{red}%20h^{n-1}}])
이제, 맨 앞의 h/h 는 약분되어 사라지고, 두번째 항부터의 h는 극한에 따라 0이 되어 사라진다.
따라서 남는 것은,

지수가 자연수 일 때 다항식의 미분은 f'(x) = nxn-1 이다.
Theorem 6.1 도함수의 기본 공식
다항식의 미분이 위와 같이 성립됨을 보았으니, 이제 몇가지 기본 공식에 대한 정리이다.
y=f(x)와 y=g(x)가 미분 가능할 때 다음과 같은 공식이 성립된다. (k는 임의의 실수이다.)
1. (f(x) ± g(x))' = f'(x) ± g'(x)
2. (kf(x))' = kf'(x)
3. (f(x)g(x))' = f'(x)g(x) + f(x)g'(x)
4.}{g(x)}%20\end{pmatrix}'=\frac{f'(x)g(x)-f(x)g'(x)}{\begin{Bmatrix}%20g(x)%20\end{Bmatrix}^{2}}) (단, g(x)≠0 이다.)
(단, g(x)≠0 이다.)
이처럼 함수끼리의 사칙연산에 대한 미분은 위와 같이 성립한다.
도함수를 찾는 과정을 미분differentiation이라고 한다. 이의 역과정을 역도함수antidifferentiation, 부정적분indefinite integral이라고 한다. 미적분학의 기본 정리는 역도함수가 적분과 같다고 말한다. 미분과 적분은 단일 변수 미적분학의 두개의 기본 연산이다.
여러 함수들의 미분을 다루는데 있어 가장 기본이 되는 다항식의 미분을 생각해보자.
n∈N 일 때, 함수 f(x)=xn 이라고 하자. 그러면 f'(x)는 정의에 따라,
가 된다.
다항함수를 전개하면,
빨갛게 표시한 항은 같으므로 0이 되고 h 항을 중심으로 정리하면,
이제, 맨 앞의 h/h 는 약분되어 사라지고, 두번째 항부터의 h는 극한에 따라 0이 되어 사라진다.
따라서 남는 것은,
지수가 자연수 일 때 다항식의 미분은 f'(x) = nxn-1 이다.
Theorem 6.1 도함수의 기본 공식
다항식의 미분이 위와 같이 성립됨을 보았으니, 이제 몇가지 기본 공식에 대한 정리이다.
y=f(x)와 y=g(x)가 미분 가능할 때 다음과 같은 공식이 성립된다. (k는 임의의 실수이다.)
1. (f(x) ± g(x))' = f'(x) ± g'(x)
2. (kf(x))' = kf'(x)
3. (f(x)g(x))' = f'(x)g(x) + f(x)g'(x)
4.
이처럼 함수끼리의 사칙연산에 대한 미분은 위와 같이 성립한다.
다항식의 미분(정수)
위에서는 다항식의 차수가 자연수일 때 미분이 성립함을 보였다. 하지만 다항식의 미분은 차수가 정수일 때도 성립하는데, 성립이 어떻게 되는지 아래에 보이겠다.
n∈Z 일 때, 함수 f(x)=xn를 미분하자.
먼저, 1) n=0 일 때, f(x)=1 이므로 미분하면 0이 된다.
2) m이 자연수이고, n=-m 이라면 이 된다.
따라서, n이 정수일 때도 다항식은 미분이 가능하다.
합성함수 미분법
연쇄법칙(연쇄율, Chain rule)은 라이프니츠Leibniz가 처음으로 사용했다. 라이프니츠는 함수 a+bz+cz2와 제곱근 함수의 합성함수인 의 도함수를 구할 때 사용했다. 그는 그의 전기에서 이것을 구할 때 수많은 실수를 했었다고 처음 밝혔다. 로피탈L'Hôpital은 그의 책 Analyse des infiniment petits에서 은연중에 사용했다. 라이프니츠의 발견이 백년이 넘게 지났어도 오일러의 해석학 책에서는 연쇄법칙이 나타나지 않는다.
Theorem 6.2 연쇄법칙, Chain rule
두 함수 u=g(x), y=f(u)가 미분 가능하다면(즉, 와,
가 존재한다.), 다음이 성립한다.
즉, 이다.
'Mathematics > General Mathematics' 카테고리의 다른 글
| 행렬의 연산과 용어, Basics Matrices and Vectors (1) | 2014.10.25 |
|---|---|
| 도함수, Derivative (3) | 2013.07.08 |
| 연속 함수, Continuous function (0) | 2013.03.30 |
| 함수의 극한, Limit of a Function (0) | 2012.05.21 |
| 함수, Function (1) | 2012.05.01 |

