미적분학에서 극한은 가장 중요한 개념이다. 극한은 함수의 어느 한 점 근방에서의 움직임 또는 무한대에서의 움직임을 관찰할 수 있는 강력한 도구이다.
17, 18세기에 미적분학의 발전이 일어났지만 함수의 극한에 대한 현대적인 개념은 1817년에 '입실론-델타'를 사용한 정의의 기본을 영국의 수학자 Bolzano가 만들때까지 기다려야했다. 하지만 이 개념은 그가 살아있을 때는 빛을 보지 못했다. Cauchy는 1821년에 그의 저서 「Cours d'analyse」에서 근본적인 현대적인 정의를 논의했지만 오직 말로만 표현한 정의였기 때문에 널리 인지되진 못했다. Weierstrass가 처음으로 극한의 '입실론-델타' 정의를 현재 우리가 쓰는 형태로 소개했고, lim와 limx→x0 도 그가 처음으로 사용했다. 현재 우리가 쓰는 lim아래에 화살표로 표현하는 방법은 1908년 Hardy가 쓴 「A Course of Pure Mathematics」에서 처음으로 나온다.
정의, Definition 3.1
모든 ε(입실론, epsilon)과 |x-a|<δ에 대하여, |f(x)-L|<ε이 성립하는 양수 δ(델타, delta)가 존재하면
=L) 으로 정의한다.
으로 정의한다.
모든 ε(입실론, epsilon)과 |x-a|<δ에 대하여, |f(x)-L|<ε이 성립하는 양수 δ(델타, delta)가 존재하면
극한의 정의는 위와 같으나 이 글에서는 오로지 직관에 의한 극한만을 생각하겠다.
함수 y=f(x)가 있다고 하자. 그러면 x가 a보다 큰 쪽에서 a로 가까워짐에 따라 함숫값 f(x)가 A로 가까워진다고 하자. 이 때 좌표평면 상에서 x의 오른쪽에서 접근하기 때문에 A를 f(x)의 x=a에서의 우극한, right-hand limit라고 하고 기호로 표현하면 아래와 같다.
이번에는 x가 a보다 작은 쪽에서 a로 가가워짐에 따라 함숫값 f(x)가 B로 가까워진다고 하자. 이 때 좌표평면 상에서 x의 왼쪽에서 접근하기 때문에 B를 f(x)의 x=a에서의 좌극한, left-hand limit라고 하고 기호로 표현하면 아래와 같다.
어느쪽에서 접근하더라도 A와 B가 같은 L이라는 값으로 접근한다면 L을 함수 f(x)의 x=a에서의 극한, limit라고 하며 이를 기호로 표현하면 아래와 같다.
A와 B가 서로 다른 값이라면 우리는 극한이 존재하지 않는다고 한다. 오로지 우극한과 좌극한의 값이 같을 때에만 극한값이 존재한다고 한다.
y=[x]라는 함수가 있다. [x] 는 Gauss 기호로 x를 넘지 않는 최대의 정수로 정의된다. 즉 1.42 면 1이 함숫값이 되고, -2.34면 -3이 함숫값이 되는 함수이다. x=0에서의 극한값을 살펴보자.
먼저 0의 좌극한은 다음과 같다.
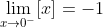
또 0의 우극한은 다음과 같다.
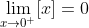
우극한과 좌극한의 값이 서로 다르다. 따라서 [x]의 x=0에서의 극한값은 없다.
먼저 0의 좌극한은 다음과 같다.
또 0의 우극한은 다음과 같다.
우극한과 좌극한의 값이 서로 다르다. 따라서 [x]의 x=0에서의 극한값은 없다.
극한을 계산할 때에 자주 쓰이는 성질들은 다음과 같다.
함수 y=f(x) 와 y=g(x)가 x=a에서 극한값을 각각 A와 B으로 갖는다. 그러면 다음 식들이 성립한다.
k라는 임의의 상수가 f(x)에 곱해져있다면,
A에 k배 곱한 것이 극한값이 된다.
또 극한의 사칙연산들도 성립한다. 덧셈과 뺄셈은 아래와 같다.
곱셈도 아래처럼 성립한다.
B가 0이 아니라면 나눗셈도 성립한다.
또 합성함수의 극한에 대해서도 아래의 성질이 성립한다.
함수 g(x)의 x=a에서의 극한값이 L이고, 함수 f(t)의 t=L에서의 극한값이 f(L) 이라면,
10의 제곱근들을 구해보자.
| 101/2 | = | 3.16227766 | |||||||||||||
| 101/4 | = | 1.77827941 | |||||||||||||
| 101/8 | = | 1.333521432 | |||||||||||||
| 101/16 | = | 1.154781985 | |||||||||||||
| 101/32 | = | 1.074607828 | |||||||||||||
| 101/64 | = | 1.036632928 | |||||||||||||
| 101/128 | = | 1.018151722 | |||||||||||||
| 101/256 | = | 1.009035045 | |||||||||||||
| 101/512 | = | 1.004507364 | |||||||||||||
| 101/1024 | = | 1.002251148 | |||||||||||||
| 101/2048 | = | 1.001124941 | |||||||||||||
| 101/4096 | = | 1.000562313 | |||||||||||||
| 101/8192 | = | 1.000281117 | |||||||||||||
| 101/16384 | = | 1.000140549 | |||||||||||||
| 101/32768 | = | 1.000070272 | |||||||||||||
| 101/65536 | = | 1.000035135 | |||||||||||||
10의 지수가 반으로 줄 때마다, 소숫점 이하의 숫자도 거의 절반으로 줄어든다. 즉, 지수와 소숫점 이하의 숫자가 비례한다. 지수와 소숫점 이하의 숫자의 비례상수를 구해보자.
| 1024 | ×0.002251148 | =2.30517585 |
| 2048 | ×0.001124941 | =2.30387999 |
| 4096 | ×0.000562313 | =2.30323242 |
| 8192 | ×0.000281117 | =2.30290873 |
| 16384 | ×0.000140549 | =2.30274690 |
| 32768 | ×0.000070272 | =2.30266600 |
| 65536 | ×0.000035135 | =2.30262554 |
| 131072 | ×0.000017567 | =2.30260532 |
2.302.... 로 되는 것이 비례상수 임을 알 수 있다. 비례 상수를 사용하여 10의 제곱근들을 다음과 같이 표현할 수 있다.
t가 0으로 접근해가면 위 식은 등식이 된다. 비례 상수를 1로 만들기 위해서 t 대신 t/2.302…를 사용하자.
이제 101/2.302… 라는 보기 불편한 숫자 대신, e라는 문자로 표현을 하면 다음과 같이 된다.
양변에 t 제곱근을 씌우면,
그런데 t가 0에 가까우면 등식이 성립하므로 극한을 취해주면 다음과 같이 된다.
이것이 바로 자연상수 e의 정의가 된다.
정의, Definition 3.2
자연상수, Euler's number 는 다음과 같이 정의한다.
^\frac{1}{t}) 이렇게 정의된 e의 값은 다음과 같다.
이렇게 정의된 e의 값은 다음과 같다.
e = 2.7182 8182 8459 0452 3536 0287 4713 5266 2497 7572 4709 3699 95…
자연상수, Euler's number 는 다음과 같이 정의한다.
e = 2.7182 8182 8459 0452 3536 0287 4713 5266 2497 7572 4709 3699 95…
'Mathematics > General Mathematics' 카테고리의 다른 글
| 도함수, Derivative (3) | 2013.07.08 |
|---|---|
| 연속 함수, Continuous function (0) | 2013.03.30 |
| 함수, Function (1) | 2012.05.01 |
| 수열, Sequence (0) | 2012.04.30 |
| 여러가지 미분법 (1) | 2009.11.05 |