어떤 두 집합 X, Y가 있다고 하자. X를 이루는 각각의 원소에 Y의 원소 하나씩을 대응시키는 것을 함수, Function이라고 한다. 이렇게 대응시키는 규칙을 기호로 표현하면 다음과 같다.
f : X → Y
그러면 X는 함수 f의 정의역, domain 이라 하고, Y는 공역, codomain이라고 한다. 함수 f에 대해 X의 원소 x에 대응되는 Y의 원소를 f(x)로 표현한다. f(x)를 함숫값, value라고 하고 함숫값들의 집합을 {f(x)|x∈x}로 표현하는데, 이 집합을 함수 f의 치역, range라고 한다.
집합 {(x,f(x)|x∈X}를 함수 f의 그래프, graph라고 한다.
그래프는 X와 Y의 곱집합,Cartesian product인 X×Y={(x,y)|x∈X,y∈Y}의 부분집합에 해당한다.
함수는 여러 종류가 존재하는데, 정의역 X의 서로 다른 두 원소 x1, x2가 있다. 이 때 함숫값 f(x1)와 f(x2)가 다르다면 우리는 이 함수를 일대일함수, 단사함수, one to one function, injective function이라고 부른다.
한편 치역과 공역이 같은 함수를 전사함수, onto function, surjective function이라고 부른다. 이 두 관계를 모두 만족하는 것을 일대일 대응, 전단사함수, one to one correspondence, bijective function라고 부른다.
단사함수, 전사함수, 전단사함수의 관계를 간단히 나타내면 다음과 같다.
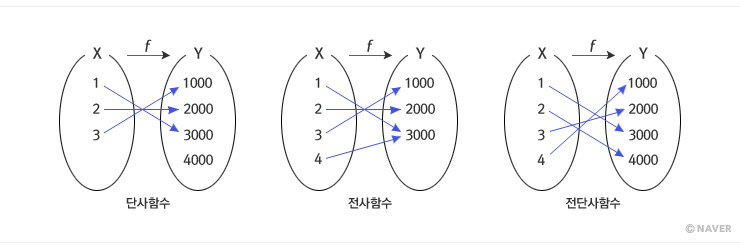
사진 출처 네이버캐스트(출처 Link)
일대일 대응인 f : X → Y가 주어졌을 때 함숫값 y를 결정하는 x가 단 하나씩만 존재하게 된다. 위의 그림을 예로 들면 1000을 결정하는 것은 4, 2000을 결정하는 것은 3인 것처럼. 그러면 역으로 Y → X로 되는 함수도 생각할 수 있는데, 이를 기호로 f -1(y)로 표현한다. 즉 f -1 : Y → X인 함수로 f -1를 f의 역함수, inversion function 이라고 한다. 역함수가 존재하려면 f가 일대일대응이여야 한다.
Theorem 2.1
함수 f : X → Y에 대해 f의 역함수 f -1가 존재할 필요충분조건은 f가 일대일대응, 전단사함수일 것이다.
f (x) = y⇔ f -1(y)=x
함수 y=f(x)가 있다고 할 때, x를 독립 변수,independent variable이라 하고 y를 종속 변수, dependent variable이라고 한다. 함수의 그래프는 R2=R×R 의 부분집합으로, R은 실수 전체 집합을 의미한다. 실수의 부분 집합을 앞으로는 다음과 같이 간략히 표현한다.
[a,b] = {x|a≤x≤b}
(a,b) = {x|a<x<b}
[a,b) = {x|a≤x<b}
(-∞,∞) = {x|-∞<x<∞} = R
[a,∞) = {x|a≤x<∞}
(a,b) = {x|a<x<b}
[a,b) = {x|a≤x<b}
(-∞,∞) = {x|-∞<x<∞} = R
[a,∞) = {x|a≤x<∞}
이와 같은 부분 집합을 구간, interval이라 하고 양끝이 포함되는 [a,b]와 같은 것을 폐구간, closed interval이라 하고, (a,b)처럼 양끝이 포함되지 않는 것을 개구간, open interval이라고 한다.
함수는 서로 연산할 수 있다. f와 g가 함수이고 c가 실 수 일때, 다음과 같이 함수의 연산을 할 수 있다.
'Mathematics > General Mathematics' 카테고리의 다른 글
| 연속 함수, Continuous function (0) | 2013.03.30 |
|---|---|
| 함수의 극한, Limit of a Function (0) | 2012.05.21 |
| 수열, Sequence (0) | 2012.04.30 |
| 여러가지 미분법 (1) | 2009.11.05 |
| 평균 변화율, 미분계수 및 도함수 (0) | 2009.11.05 |